A \(\mathcal{V}\) category, given a symmetric monoidal preorder \(\mathcal{V}=(V,\leq,I,\otimes)\)
To specify the category \(\mathcal{X}\), one specifies:
A set \(Ob(\mathcal{X})\) whose elements are called objects
A hom-object for every pair of objects in \(Ob(\mathcal{X})\), written \(\mathcal{X}(x,y) \in V\)
The following properties must be satisfied:
\(\forall x \in Ob(\mathcal{X}):\) \(I \leq \mathcal{X}(x,x)\)
\(\forall x,y,z \in Ob(\mathcal{X}):\) \(\mathcal{X}(x,y)\otimes\mathcal{X}(y,z) \leq \mathcal{X}(x,z)\)
We call \(\mathcal{V}\) the base of enrichment for \(\mathcal{X}\) or say that \(\mathcal{X}\) is enriched in \(\mathcal{V}\).
Consider the following preorder:
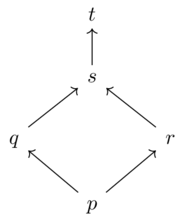
As a Bool-category, the objects are \(Ob(\mathcal{X})=\{p,q,r,s,t\}\).
For every pair, we need an element of Bool, so make it true if \(x\leq y\)
\(true\) is the monoidal unit of Bool, and this obeys the two constraints of a \(\mathcal{V}\) category.
We can represent the binary relation (hom-object) with a table:
| \(\leq\) | p | q | r | s | t |
|---|---|---|---|---|---|
| p | T | T | T | T | T |
| q | F | T | F | T | T |
| r | F | F | T | T | T |
| s | F | F | F | T | T |
| t | F | F | F | F | T |